O ábaco é um instrumento utilizado para fazer cálculos. Ele é formado por arames paralelos e com elementos de contagem, que podem ser bolinhas, por exemplo. Esse instrumento surgiu há cerca de 5500 anos atrás na Mesopotâmia. Sua forma de cálculo é por sistema decimal. Em alguns lugares esse instrumento ainda é usado nos dias de hoje para ensinar duas operações básicas da matemática: soma e subtração.
O Ábaco foi muito utilizado na antiguidade. Uma variedade desse instrumento foi desenvolvida pelas nações intelectuais. Por isso temos na história os ábacos mesopotâmico, babilônico, egípcio, romano, indiano, chinês, japonês, russo, escolar e para deficientes visuais.
Em uma competição de matemática, alguns alunos conseguiram fazer contas complexas de forma mais rápida com um ábaco enquanto seus oponentes usavam uma calculadora eletrônica.
CONSTRUÇÃO E UTILIZAÇÃO DO ÁBACO
Cada bastão contém bolas móveis, que podem ser movidas para cima e para baixo. Assim, de acordo com o número de bolas na posição inferior, temos um valor representado. Pode haver variações, como na figura ao lado, onde se fazem divisões na moldura e o número de bolas é alterado. Observe que na figura temos o número 6302715408 (por exemplo 8=5+3, com a parte superior representando múltiplos de 5, neste caso 0, 5 e 10).
Estrutura com hastes metálicas divididas em duas partes, das quais uma tem duas contas e a outra, cinco contas, que deslizam nessas hastes. Os ábacos orientais dispõem de varas verticais divididas em dois, com as contas sobre a barra tendo o valor cinco vezes superior aos das contas abaixo. O suanpan chinês dispõe de duas contas acima da barra ou divisor e cinco abaixo. O moderno soroban japonês por outro lado, tem uma conta acima e quatro abaixo do divisor.
Algumas hastes podem ser reservadas pelo operador para armazenar resultados intermediários. Desta forma, poucas guias são necessárias, já que o ábaco é usado mais como um reforço de memória enquanto o usuário faz as contas de cabeça.
EXEMPLO DE CÁLCULO
O cálculo começa à esquerda, ou na coluna mais alta envolvida em seu cálculo, e trabalha da esquerda para a direita. Assim, se tiver 548 e desejar somar 637, primeiro colocará 548 na calculadora. Daí, adiciona 6 ao 5. Segue a regra ou padrão 6 = 10 – 4 por remover o 5 na vara das centenas e adicionar 1 na mesma vara (-5 + 1 = -4) daí, adicione uma das contas de milhares à vara à esquerda. Daí, passa a somar o três ao quatro, o sete ao oito, e no ábaco aparecerá a resposta: 1.185.
Devido a operar assim, da esquerda para a direita, pode começar seu cálculo assim que saiba o primeiro dígito. Na aritmética mental ou escrita, calcula a partir das unidades ou do lado direito do problema.
HISTÓRIA DO ÁBACO

O ábaco é um antigo instrumento de cálculo, que segundo muitos historiadores foi inventado na Mesopotâmia, pelo menos em sua forma primitiva e depois os chineses e romanos o aperfeiçoaram.
Daí, uma variedade de ábacos foram desenvolvidos; o mais popular utiliza uma combinação de dois números-base (2 e 5) para representar números decimais. Mas os mais antigos ábacos usados primeiro na Mesopotâmia e depois na Grécia e no Egito por escrivães usavam números sexagesimais representados por fatores de 5, 2, 3 e 2 por cada dígito.
A palavra ábaco originou-se do Latim abacus, e esta veio do grego abakos. Esta era um derivado da forma genitiva abax (lit. tábua de cálculos). Porque abax tinha também o sentido de tábua polvilhada com terra ou pó, utilizada para fazer figuras geométricas, alguns linguistas especulam que tenha vindo de uma língua semítica (o púnico abak, areia, ou o hebreu ābāq (pronunciado a-vak), areia.
ÁBACO MESOPOTÂMICO
O primeiro ábaco foi quase de certeza construído numa pedra lisa coberta por areia ou pó. Palavras e letras eram desenhadas na areia; números eram eventualmente adicionados e bolas de pedra eram utilizadas para ajuda nos cálculos. Os babilônios utilizavam este ábaco em 2700–2300 a.C..4 A origem do ábaco de contar com bastões [1] é obscuro, mas a Índia, a Mesopotâmia ou o Egito são vistos como prováveis pontos de origem.5 A China desempenhou um papel importante no desenvolvimento do ábaco.
ÁBACO BABILÔNIO
Os babilônios podem ter utilizado o ábaco para operações de adição e subtração. No entanto, este dispositivo primitivo provou ser difícil para a utilização em cálculos mais complexos.6 Algumas pessoas conhecem um carácter do alfabeto cuneiforme babilônio que pode ter sido derivado de uma representação do ábaco.7 Por isso esse ábaco é muito importante.
ÁBACO EGÍPCIO
O uso do ábaco no antigo Egito é mencionado pelo historiador grego Crabertotous, que escreve sobre a maneira do uso de discos (ábacos) pelos egípcios, que era oposta na direção quando comparada com o método grego. Arqueologistas encontraram discos antigos de vários tamanhos que se pensam terem sido usados como material de cálculo. No entanto, pinturas de parede não foram descobertas, espalhando algumas dúvidas sobre a intenção de uso deste instrumento.
ÁBACO GREGO
Uma tábua encontrada na ilha grega de Salamina em 1846 data de 300 a.C., fazendo deste o mais velho ábaco descoberto até agora. É um ábaco de mármore de 149 cm de comprimento, 75 cm de largura e de 4,5 cm de espessura, no qual existem 5 grupos de marcações. No centro da tábua existe um conjunto de 5 linhas paralelas igualmente divididas por uma linha vertical, tampada por um semicírculo na intersecção da linha horizontal mais ao canto e a linha vertical única. Debaixo destas linhas, existe um espaço largo com uma rachadura horizontal a dividi-los. Abaixo desta rachadura, existe outro grupo de onze linhas paralelas, divididas em duas secções por uma linha perpendicular a elas, mas com o semicírculo no topo da intersecção; a terceira, sexta e nona linhas estão marcadas com uma cruz onde se intersectam com a linha vertical.
ÁBACO ROMANO

O método normal de cálculo na Roma antiga, assim como na Grécia antiga, era mover bolas de contagem numa tábua própria para o efeito. As bolas de contagem originais denominavam-se calculi. Mais tarde, e na Europa medieval, os jetons começaram a ser manufacturados. Linhas marcadas indicavam unidades, meias dezenas, dezenas, etc., como na numeração romana. O sistema de contagem contrária continuou até à queda de Roma, assim como na Idade Média e até ao século XIX, embora já com uma utilização mais limitada.
Em adição às mais utilizadas bolas de contagem frouxas, vários espécimens de um ábaco romano foram encontrados, mostrados aqui em reconstrução. Tem oito longos sulcos contendo até 5 bolas em cada e 8 sulcos menores tendo tanto uma como nenhuma bola.
Nos sulcos menores, o sulco marcado I marca unidades, o X dezenas e assim sucessivamente até aos milhões. As bolas nos sulcos menores marcam os cincos – cinco unidades, cinco dezenas, etc. – essencialmente baseado na numeração romana. As duas últimas colunas de sulcos serviam para marcar as subdivisões da unidade monetária. Temos de ter em conta que a unidade monetária se subdividia em 12 partes, o que implica que o sulco longo marcado com o sinal 0(representando os múltiplos da onça ou duodécimos da unidade monetária) comporte um máximo de 5 botões, valendo cada uma 1 onça, e que o botão superior valha 6 onças. Os sulcos mais pequenos à direita são fracções da onça romana sendo respectivamente, de cima para baixo, ½ onça, ¼ onça e ⅓ onça.
ÁBACO INDIANO
Fontes do século I, como a Abhidharmakosa, descrevem a sabedoria e o uso do ábaco na Índia. Por volta do século V, escrivães indianos estavam já à procura de gravar os resultados do Ábaco. Textos hindus usavam o termo shunya (zero) para indicar a coluna vazia no ábaco.
ÁBACO CHINES
A menção mais antiga a um suanpan (ábaco chinês) é encontrada num livro do século I da Dinastia Han Oriental, o Notas Suplementares na Arte das Figuras escrito por Xu Yue. No entanto, o aspecto exacto deste suanpan é desconhecido.
Habitualmente, um suanpan tem cerca de 20 cm de altura e vem em variadas larguras, dependendo do fabricante. Tem habitualmente mais de sete hastes. Existem duas bolas em cada haste na parte de cima e cinco na parte de baixo, para números decimais e hexadecimais. Ábacos mais modernos tem uma bola na parte de cima e quatro na parte de baixo. As bolas são habitualmente redondas e feitas em madeira. As bolas são contadas por serem movidas para cima ou para baixo. Se as mover para o alto, conta-lhes o valor; se não, não lhes conta o valor. O suanpan pode voltar à posição inicial instantaneamente por um pequeno agitar ao longo do eixo horizontal para afastar todas as peças do centro.
Os suanpans podem ser utilizados para outras funções que não contar. Ao contrário do simples ábaco utilizado nas escolas, muitas técnicas eficientes para o suanpan foram feitas para calcular operações que utilizam a multiplicação, a divisão, a adição, a subtração, a raiz quadrada e a raiz cúbica a uma alta velocidade.
No famoso quadro Cenas à Beira-mar no Festival de Qingming pintado por Zhang Zeduan (1085-1145) durante a Dinastia Song (960-1297), um suanpan é claramente visto ao lado de um livro de encargos e de prescrições do doutor na secretária de um apotecário.
A similaridade do ábaco romano com o suanpan sugere que um pode ter inspirado o outro, pois existem evidências de relações comerciais entre o Império Romano e a China. No entanto, nenhuma ligação direta é passível de ser demonstrada, e a similaridade dos ábacos pode bem ser coincidência, ambos derivando da contagem de cinco dedos por mão. Onde o modelo romano tem 4 mais 1 bolas por espaço decimal, o suanpan padrão tem 5 mais 2, podendo ser utilizado com números hexadecimais, ao contrário do romano. Em vez de funcionar em cordas como os modelos chinês e japonês, o ábaco romano funciona em sulcos, provavelmente fazendo os cálculos mais difíceis.
Outra fonte provável do suanpan são as pirâmides numéricas chinesas, que operavam com o sistema decimal mas não incluíam o conceito de zero. O zero foi provavelmente introduzido aos chineses na Dinastia Tang (618-907), quando as viagens no Oceano Índico e no Médio Oriente teriam dado contacto direto com a Índia e o Islão, permitindo-lhes saber o conceito de zero e do ponto decimal de mercantes e matemáticos indianos e islâmicos.
O suanpan migrou da China para a Coreia em cerca do ano 1400. Os coreanos chamam-lhe jupan (주판), supan (수판) or jusan (주산).
ÁBACO JAPONÊS
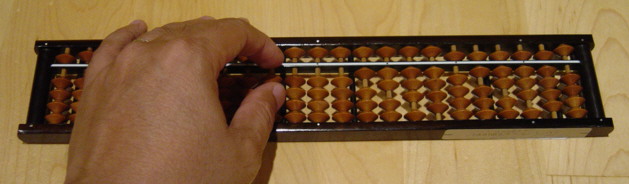
Um soroban (算盤, そろばん, lit. tábua de contar) é uma versão modificada pelos japoneses do suanpan. É planeado do suanpan, importado para o Japão antes do século XVI.15 No entanto, a idade de transmissão exata e o meio são incertos porque não existem registos específicos.16 17 Como o suanpan, o soroban ainda hoje é utilizado no Japão, apesar da proliferação das calculadoras de bolso, mais baratas.
A Coreia tem também o seu próprio, o supan (수판), que é basicamente o soroban antes de tomar a sua atual forma nos anos 30. O soroban moderno também tem este nome
ÁBACO DOS NATIVOS AMERICANOS
Algumas fontes mencionam o uso de um ábaco chamado nepohualtzintzin na antiga cultura azteca. Este ábaco mesoamericano utiliza um sistema de base 20 com 5 dígitos.
O quipu dos Incas era um sistema de cordas atadas usado para gravar dados numéricos, como varas de registo avançadas – mas não eram usadas para fazer cálculos. Os cálculos eram feitos utilizando uma yupana (quechua para tábua de contar), que estava ainda em uso depois da conquista do Peru. O princípio de trabalho de uma yupana é desconhecido, mas, em 2001, uma explicação para a base matemática deste instrumento foi proposta. Por comparação à forma de várias yupanas, os investigadores descobriram que os cálculos eram baseados na sequência Fibonnaci, utilizando 1,1,2,3,5 e múltiplos de 10, 20 e 40 para os diferentes campos do instrumento. Utilizar a sequência Fibonnaci manteria o número de bolas num campo no mínimo.
ÁBACO RUSSO

O ábaco russo, o schoty (счёты), normalmente tem apenas um lado comprido, com 10 bolas em cada fio (excepto um que tem 4 bolas, para fracções de quartos de rublo). Este costuma estar do lado do utilizador. (Modelos mais velhos têm outra corda com 4 bolas, para quartos de kopeks, que eram emitidos até 1916. O ábaco russo é habitualmente utilizado na vertical, com os fios da esquerda para a direita ao modo do livro. As bolas são normalmente curvadas para se moverem para o outro lado no centro, em ordem para manter as bolas em cada um dos lados. É clarificado quando as bolas se devem mover para a direita. Durante a manipulação, as bolas são movidas para a direita. Para mais fácil visualização, as duas bolas do meio de cada corda (a 5ª e a 6ª; no caso da corda excepção, a 3ª e a 4ª) costumam estar com cores diferentes das outras oito. Como tal, a bola mais à esquerda da corda dos milhares (e dos milhões, se existir) costuma também estar pintada de maneira diferente.
O ábaco russo estava em uso em todas as lojas e mercados de toda a antiga União Soviética, e o uso do ábaco era ensinado em todas as escolas até aos anos 90. Hoje é visto como algo arcaico e foi substituído pela calculadora. Na escola, o uso da calculadora é ensinado desde os anos 90.
ÁBACO ESCOLAR
Em todo o mundo, os ábacos têm sido utilizados na educação infantil e na educação básica como uma ajuda ao ensino do sistema numérico e da aritmética. Nos países ocidentais, uma tábua com bolas similar ao ábaco russo mas com fios mais direitos e um plano vertical tem sido comum (ver imagem).
O tipo de ábaco aqui mostrado é vulgarmente utilizado para representar números sem o uso do lugar da ordem dos números. Cada bola e cada fio tem exactamente o mesmo valor e, utilizado desta maneira, pode ser utilizado para representar números até 100.
A vantagem educacional mais significante em utilizar um ábaco, ao invés de bolas ou outro material de contagem, quando se pratica a contagem ou a adição simples, é que isso dá aos estudantes uma ideia dos grupos de 10 que são a base do nosso sistema numérico. Mesmo que os adultos tomem esta base de 10 como garantida, é na realidade difícil de aprender. Muitas crianças de 6 anos conseguem contar até 100 de seguida com somente uma pequena consciência dos padrões envolvidos.
USO PELOS DEFICIENTES VISUAIS
Um ábaco adaptado, inventado por Helen Keller e chamado de Cranmer, é ainda utilizado por deficientes visuais. Um pedaço de fabrico suave ou borracha é colocado detrás das bolas para não moverem inadvertidamente. Isto mantém as bolas no sítio quando os utilizadores as sentem ou manipulam. Elas utilizam um ábaco para fazer as funções matemáticas multiplicação, divisão, adição, subtração, raiz quadrada e raiz cúbica.
Embora alunos deficientes visuais tenham beneficiado de calculadoras falantes, o uso do ábaco é ainda ensinado a estes alunos em idades mais novas, tanto em escolas públicas como em escolas privadas de ensino especial. O ábaco ensina competências matemáticas que nunca poderão ser substituídas por uma calculadora falante e é uma ferramenta de ensino importante para estudantes deficientes visuais. Os estudantes deficientes visuais também completam trabalhos de matemática utilizando um escritor de Braille e de código Nemeth (uma espécie de código Braille para a matemática), mas as multiplicações largas e as divisões podem ser longas e difíceis. O ábaco dá a estudantes deficientes visuais e visualmente limitados uma ferramenta para resolver problemas matemáticos que iguala a velocidade dos seus colegas sem problemas visuais utilizando papel e lápis. Muitas pessoas acham esta uma máquina útil durante a sua vida.
BIBLIOGRAFIA
Edwin D. Reilly; William Leonard Langer. Concise Encyclopedia of Computer Science. [S.l.]: John Wiley and Sons, 2004. ISBN 0470090952
Thomas William Körner; William Leonard Langer. The Pleasures of Counting. [S.l.]: Houghton Mifflin Books, 1996. ISBN 0521568234
Richard Anthony Mollin. Fundamental Number Theory with Applications. [S.l.]: CRC Press, 1998. ISBN 0849339871
David Eugene Smith. History of Mathematics. [S.l.]: Courier Dover Publications. vol. 2. ISBN 0486204308
Thomas Crump. The Japanese Numbers Game: The Use and Understanding of Numbers in Modern Japan. [S.l.]: Routledge, 1992. ISBN 0415056098
Ettore Carruccio. Mathematics And Logic in History And in Contemporary Thought. [S.l.]: Aldine Transaction, 2006. ISBN 0202308502
Peter N. Stearns; William Leonard Langer. The Encyclopedia of World History: Ancient, Medieval, and Modern, Chronologically Arranged. [S.l.]: Houghton Mifflin Books, 2001. ISBN 0395652375
Peng Yoke Ho. Li, Qi and Shu: An Introduction to Science and Civilization in China. [S.l.]: Courier Dover Publications, 2000. ISBN 0486414450
Merriam-Webster’s Collegiate Dictionary. 11 ed. [S.l.]: Merriam-Webster, Inc, 2003. ISBN 0877798095
Oxford English Dictionary: “abacus”. 2 ed. [S.l.]: Universidade de Oxford, 1989.
The History of the Abacus. Londres: Books That Matter, 1968. ISBN 0090894103

